Arithmetic Logic Unit: ALU

Instead of explaining how to build an ALU, I will show you one.
Behold the glory of SN74LS181:

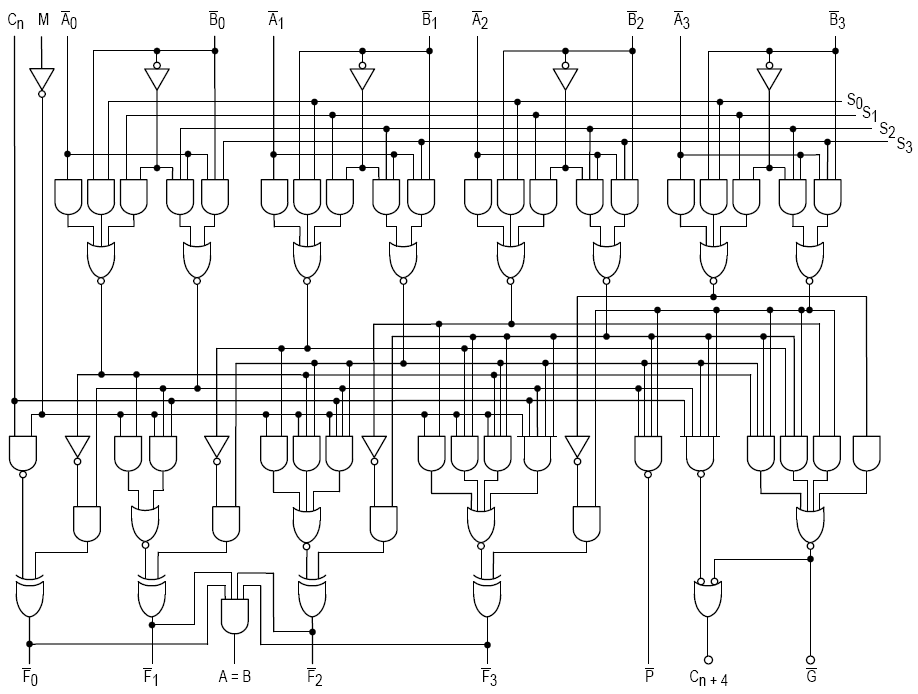
The output is purely feed-forward, series of transformations that given an input, perform certain operations and then produces an output. The symbols on the schematics are various gates, all signals flow from top to bottom. This ALU unit can perform 4 bit operations.

You select what function to use with S0-S4, M is used to choose between logical or arithmetic operations, A0-A3 is one input and B0-B3 is the other, the operation is done bit by bit A0 with B0, A1 with B1, A2 with B2, A3 with B3. You get the output from the bottom F0-F3.

Lets add 5 and 9.

5: 0101
9: 1001

Preparing the input:

A3: 0    B3: 1
A2: 1    B2: 0
A1: 0    B1: 0
A0: 1    B0: 1

M: 1 for arithmetic mode

S: 1001, for A + B

S3: 1
S2: 0
S1: 0
S0: 1

------

Output:

F3: 1
F2: 1
F1: 1
F0: 0

First let's do the addition by hand

  
  3210
  
  0101 (A: 5)
+ 1001 (B: 9)
-------
  1110 (14)
  ||||
  ||| `-> 1 + 1 = 10, 0 and we carry 1
  |||
  ||`---> 0 + 0 + 1(carry) = 1, nothing to carry
  || 
  |`----> 1 + 0 = 1, nothing to carry
  |
  `-----> 0 + 1 = 1, nothing to carry

You can see in the diagram, how A0 with B0's carry gets to A1 and B1 and etc, in the end you can see A3 with B3's carry gets to the Cn+4 output, which can be put in the Cn input of a next chip, you can chain multiple 74181 ALU units to make operations on more bits.

This is a list of all the things this amazing chip can do:

I want to emphasize again, this is the first circuit that we discuss is not actually a loop, but a complete feed forward transformation. And you can see how with very few elements it can do so many different things! Every time I look at it I am amazed.

When we are building our hypothetical computer, we would connect 2 of those, one after the other, so that we can do 8 bit operations. And we will hook our registers to it. We will have an instructions which will make the control unit load data into registers, then the next instruction will make it use the registers data and pass it to the ALU, after which will take the output of the ALU and put it on the bus.

https://people.ee.duke.edu/~jab/ece52/datasheets/sn74ls181.pdf

But how does it work? How can we do math through a feed forward stream of information?

The magic of the ALU is in the way it uses logic gates (AND, OR, NOR, XOR, NAND etc). You saw in the beginning of the chapter how to build SR Latches and Flip Flops and store bits of information, and now I will show you how to do addition, and you will see that subtraction is also addition, and multiplication is also addition and division is also addition.. and negative numbers are made up.

One and Zero are the only true numbers! MUAHAHAH.

The following circuit can perform addition of 2 bits A and B plus a carry bit Cin , and produce a result S and a carry bit Cout

This is the NAND truth table, I will leave you to try out the circuit yourself, try to add 1 + 0 with carry 1, and 1 + 1 with carry 1.

| X | Y | Q = NAND(X,Y) |
|---|---|---------------|
| 0 | 0 | 1             |
| 0 | 1 | 1             |
| 1 | 0 | 1             |
| 1 | 1 | 0             |

We want to add numbers that can be represented by 32 or even 64 bits, so we can just chain a bunch of adders.

The carry out of one becomes the carry in of the next. In this image you can see the least significant bit, is on the right, and the most significant bit is on the left.

place: |8|4|2|1|
-------|-|-|-|-|
value: |1|0|0|1|

In this example, if we toggle the least significant bit, the number changes from 1001 to 1000, or from 9 to 8, but if we toggle the most significant bit, 1001 becomes 0001, or from 9 to 1.

You can see now how we can add numbers, but how can we subtract? A - B is the same as A + (-B), So we need a way to represent negative numbers -B. Knowing if a number is positive or negative is a piece of information that we need to have, and since it has exactly two possible values: positive or negative, we can use 1 bit to tell us that.

We call it the sign bit, if its 1 that means the number is negative, if its 0 that means its positive. You can see this is a huge cost, to reduce our possible number by one whole bit, if we have a 32 bit integer our maximum value is 4294967295, but if we have 31 bit integer the maximum value is 2147483647, but we can have negative values. That is why in C we have the unsigned keyword, so that we can create unsigned long, int, char, etc data types, to allow to decide when we want to pay the price of the sign bit, in go you also have uint and int, but in java all primitive integers are signed.

You might think that we just put the bit on or off and thats enough, which seem to work when you look at it.

But, if you try to add 5 + -5 you will see it does not work:

  0101
  1101
  ----
 10010
 ^
 this bit is cut off since we don't have space
 in our 4 bit computer

So 5 - 5 is equal to 2, which.. is not good, and would lead to the absolute collapse of the universe if it were true. It is weird to think what holds our universe together, but one of the things seems to be that 5 - 5 is 0.

There is a way to make the math work out, by inverting the bits of the negative numbers, so 1 becomes from 0001 to 1110, and so on. There is a slight weirdness with 0, we have it both as +0 and as -0, but at least the math checks out.

So 5 - 5 is:

Which is -0, much better than +2 we had before, lets try another subtraction 5 - 3.

So the result is 1, which is again not amazing, but we just need to add 1 to it to get to the right value. You can try it with other numbers and will see you are always missing 1. This method is called One's complement. So A + (-B) is (A + NOT(B)) + 1, it works and some systems use it, but it is quite annoying with this -0 business.

Most systems use even better method called Two's complement

The way we do A + (-B) is using Two's Complement, which just removes the -0, and replaces it with -1

To convert a number to its negative you need to do NOT(B) + 1, so 3 becomes 0011 -> 1100 and we add 1 => 1101.

This way everything works out just fine.

So 5 - 5 is:

  0101
  1011
  ----
 10000
 ^
 cut

Which is -0, much better than +2 we had before, lets try another subtraction 5 - 3.

  0101
  1101
  ----
 10010
 ^
 cut

It works out to 2. So negating a number is NOT(B) + 1, and A - B is A + (NOT(B) + 1).

Make sure you watch Ben Eater's Two's Complement video, I copied the examples from there so that you are familiar when you watch it.

But how would we do multiplication and division, and what about fractions? I will briefly discuss them because they can easilly take over the whole book. Multiplication and division by 2 are extremely natural, you can see that by just moving/shifting the bit pattern left we double the value and moving it right we halve it.

Halving:
4: 0100 
2: 0010 
1: 0001

Doubling:
1: 0001
2: 0010 
4: 0100

If we want to multiply 2 * 6, we can multiply 2 * 2 (which is easy, just moving it to the left once) and then add it to 2 * 4 (which is also easy, just moving it to the left twice), but what about 7 * 3? Well we will just have to do 7 + 7 + 7.

There are dedicated circuits that specialze in multiplication, like 74LS384. Division however is another story (unless it is division by 2), it requires way more complicated logic and multiple chips and multiple clock cycles to get it done. Watch some videos of people building minecraft calculators and see their horror when they have to build the division logic with redstone.

What about fractions? There are two ways, we can do fixed point fractions, for example we dedicate few bits for the whole part, and few bits for the fraction part, in a 32 bit system we could say, 1 bit is for sign, 15 bits are for the whole part, and 16 bits are for fraction. Then we could have special instructions for adding and multiplying, and they will know exactly what to do.

Or we could use floating point numbers, which are more complicated but more flexible, 32 bit floating point numbers use 1 sign bit, 8 bit exponent and 23 bit mantissa (also called significand).

Again, we wont go into detail, but there is special circuits needed in order to efficiently do floating point math.

Since our computer only needs 1 instruction, and all it does is subtract, we could do that by using 74LS283 adder and 74LS04 inverter, or using 74LS181 ALU that we can configure to do subtraction, or we can build our own adder using NAND gates. Since I just love the 74LS181 chip, we will use it, and it also allows you to experiment and try other things.

Machine Code

Arithmetic Logic Unit: ALU