Control Unit: Part 2
We want to build a computer that can execute our program that counts to 3.
| 70 | 61 | 92 |
| 83 | 84 | 05 |
| 36 | 17 | 08 |
| 89 | 810 | 911 |
Reminder of how SUBLEQ works:
PC = 0
forever:
a = memory[PC]
b = memory[PC + 1]
c = memory[PC + 2]
memory[b] = memory[b] - memory[a]
if memory[b] <= 0:
PC = c
else
PC += 1
First you try to execute the program in your mind. You see the value at each memory location and its address: 7 is at address 0, 6 is at address 1 and so on. Use your index finger, start from the first digit and evaluate the first instruction. 7 6 9, first look at address 7 and remember the value; move your index finger to the next address, which has the value 6, look at address 6 and remember the value, now subtract from it the first value you remember, and store the result at address 6. If the result is smaller or equal to zero, you have to move your index finger to address 9 and start executing the next instruction from there, otherwise move your finger two locations over, to get to the next instruction, and do the same thing again, instruction after instruction.
There are a few key elements: first we need to make an 'index finger' somehow, we have to know which instruction we are executing. Second, we have to be able to look at an address and remember its value, we have to be able to subtract two values and then store the result, and we have to be able to check if the result is smaller or equal to zero. Depending on this we have to either move our index finger to a specific location, or move our index finger to the following instruction.
First, how do we know if we even have to if, as in, how do we know if the
result is <= 0? We know that negative numbers will have their most significant
bit as 1, and our 74LS181 also has comparator mode. It has a pin A==B that is
HIGH if the inputs are equal, or LOW if not (which only works if the chip is
in subtraction mode and carry in is 1, but turns out this is exactly the thing
we are doing). So if we just OR both those pieces of information. 74LS181 has
its inputs and outputs inverted, so we will have to use 74LS04 to invert them
back, but after we invert the output we can send the value of A==B and
INV(F3) (the inverted value of the most significant bit of the output), to an
OR gate from 74LS32, and its output will be 1 if the result of the subtraction
is 0 or negative.
We need the control unit to be able to orchestrate all those chips, enable and disable their inputs and outputs accordingly. We know how to store data with registers, we know how to do the subtraction with the ALU, we know how to count with the 74LS161 counter. We need a few temporary registers to help us with the wiring and such, but the mini operations look.
I have broken down the steps of what needs to happen in order to execute the SUBLEQ program:
Legend:
PC: Program Couner
MAR: Memory Address Register
RAM[MAR]: Value at address MAR
e.g. if MAR's value is 6,
RAM[MAR] is the value at address 6
START:
MAR = PC
Enable PC's output to the bus
Enable MAR's C pin to latch on the bus's value
TMP = RAM[MAR]
Enable RAM's output to the bus
Enable TMP's C pin to latch on the bus's value
(MAR's output is always enabled, it is just connected
to the RAM's address pins)
MAR = TMP
Enable TMP's output to the bus
Enable MAR's C pin to latch on the bus's value
A = RAM[MAR], PC++
Enable RAM's output to the bus
Enable A's C pin to latch on the bus's value
Send a clock pulse to PC's clock pin, to increment its value
MAR = PC
Enable PC's output to the bus
Enable MAR's C pin to latch on the bus's value
TMP = RAM[MAR]
Enable RAM's output to the bus
Enable TMP's C pin to latch on the bus's value
B = RAM[MAR], PC++
Enable RAM's output to the bus
Enable B's C pin to latch on the bus's value
Send a clock pulse to PC's clock pin, to increment its value
RAM[MAR] = B - A
Enable the ALU's output to write to the bus
Enable Write Enable on the RAM to set the value at MAR address
Enable the Flag register's C pin to latch on the output of the OR gate
ENABLE FLAG
Enable the Flag register's output enable
IF FLAG == 0:
Send a clock pulse to PC's clock pin, to increment its value
GOTO START
IF FLAG == 1:
MAR = PC
Enable PC's output to the bus
Enable MAR's C pin to latch on the bus's value
TMP = RAM[MAR]
Enable RAM's output to the bus
Enable TMP's C pin to latch on the bus's value
PC = TMP
Enable TMP's output to the bus
Enable the LD pin on PC to set the value
GOTO START
We will use a sequencer, a simple counter to allow us to step through those micro instructions. We could then have a matrix of wires, where it enables or disables specific pins on the corresponding chips, but I took another approach, we will use two EEPROMS, and will program them so that their values on specific addresses will enable or disable the appropriate chips. I think its quite nice that we have a program to execute our program.
Reminder the 28AT64C EEPROM has 12 address pins, and 8 output pins, our sequencer is just 74LS161 counter, we pulse a clock to it and it increments its value. It has 4 bit value, so we can hook its output to A0, A1, A2, A3 on both EEPROMs, and each of the output pins we will hook to different chip. The reason we need two eeproms is we just have to control many chips, and we need more than 8 control tenticles.
This is an example how one eeprom will look:

So when the sequencer is at value 0, and the flag register's output is 0, the address requested by the eeprom is 0, which means on the output we will see whatever we stored at address 0. And if we store the number 3 (00000011 in binary) at address 0 for example, then the values at each i/o pin will be:
i/o 0| 1 HIGH
----------
i/o 1| 1 HIGH
----------
i/o 2| 0 LOW
----------
i/o 3| 0 LOW
----------
i/o 4| 0 LOW
----------
i/o 5| 0 LOW
----------
i/o 6| 0 LOW
----------
i/o 7| 0 LOW
Now imagine i/o 0 is connected to the PC enable pin, and i/o 1 is connected
to the MAR C pin, we will do the first step of our SUBLEQ recipe, and store the
value of PC into MAR, or MAR = PC. Then at the next clock pulse the sequencer
will increment its value, and we will get to address 1, and whatever we stored
there will control the pins connected to the i/o lines.
The most intersting part is, you see on A4 we have connected the output of the
flag register, meaning that when we enable the flag register, for example it
could be by outputting HIGH on i/o 6, if its output value is 1, we will get
to another addres! And on this new address will have values specific to if <= 0. You see how the control logic will orchestrate the the computer, and then
the computer orchestrates the control logic. You should always pay close
attention to any system where its output modifies the system itself. It is more
common in life than you think. For example, how education develops culture, and
how culture develops education, or the relationship between the mitochondria and
the rest of the cell.
This is a more complete diagram of how the flag feeds into the control and the control manipulates the flag register's output, which changes the address and therefore the eeprom's output.

In the computer I have made I am using different pins, just because I did not
think it through, I really just wanted to get it working. If you are doing the whole
computer yourself I would recommend to just understand the concept and try to do
it without copying. There are other single instruction machines, such as SBNZ
A,B,C,D which does mem[C] = mem[B] - mem[A]; if mem[C] != 0 goto D. or you can
do a small 4 bit computer like Richard Buckland's 4917, it is quite fun, I even
made 54 programs for it https://punkx.org/4917.
You can see the computer working working and executing the SUBLEQ program here: https://www.youtube.com/watch?v=E-m9hW3x1no and my debugging timelapse https://www.youtube.com/watch?v=zuj7cGZGdQ4.
This is the Digital diagram:

We increment the sequencer by creating a good square pulse using the 555 timer in monostable mode, we press a button and it will create 1ms (depending on how we setup its resistors and capacitors) pulse to the clock input. In the real world there is also a 555 timer as the input of the PC to create again a good pulse, in the beginning I used a resistor + capacitor to create a short analog pulse, which worked like 97% of the time, just enough to cause all kinds of trouble. the 555 timer can tick as fast as 32000 times per second, but since we will manually trigger ours, our CPU will tick about 2-3 times per second, since thats how fast I press the button. Quite the contrast with your laptop which ticks about 2,000,000,000 times per second.
One thing we did not talk about, is how do we actually load the program into
ram? We could store the program in another EEPROM, and then have a small circuit
that copies it to RAM address by address, and once dont it could signal the
control EEPROMs on A6 for example, but I chose to program it manually with
switches. You can see there are two switches going to A6 and A7, and 4 switches
that are connected to the bus, To set the control in "programming" mode, I
enable ths switch to put HIGH on A6, and I put different micro instructions on
those addresess.
MAR = PC
NOTHING <-- here we can put the value on the bus without conflict
RAM[MAR] = BUS, PC += 1
NOTHING <-- here we check the RAM value with the debug LEDs
RESET SEQUENCER
If I enable both A6 and A7 we get into RAM reading mode, so that I can debug what is actually in RAM.
NOTHING <-- here we check the RAM value with the debug LEDs
MAR = PC
PC++
RESET SEQUENCER
This is the binary data uploaded to the eeproms, eeprom0 is the left one, and eeprom1 is the right one
$ hexdump eeprom0.bin
0000000 b9f1 adf9 b9f1 abf9 b938 b9a9 b9b9 b9b9
0000010 b9b9 b9b9 b9b9 b9b9 b9b9 b9f1 a989 b9b9
0000020 b9f1 b929 b9b9 b9b9 b9b9 b9b9 b9b9 b9b9
0000030 b9b9 b9b9 b9b9 b9b9 b9b9 b9b9 b9b9 b9b9
*
0000060 f1b9 b9a9 b9b9 b9b9 b9b9 b9b9 b9b9 b9b9
0000070 b9b9 b9b9 b9b9 b9b9 b9b9 b9b9 b9b9 b9b9
*
0002000
$ hexdump eeprom1.bin
0000000 5e5b 5a59 5e5b 5a59 537b 4353 dbdb dbdb
0000010 dbdb dbdb dbdb dbdb d3db 5653 4391 dbdb
0000020 db5b 5b5b db4b dbdb dbdb dbdb dbdb dbdb
0000030 dbdb dbdb dbdb dbdb dbdb dbdb dbdb dbdb
*
0000060 5bdb 4bdb dbdb dbdb dbdb dbdb dbdb dbdb
0000070 dbdb dbdb dbdb dbdb dbdb dbdb dbdb dbdb
*
0002000
If you are not familiar with hexadecimal numbers, don't worry, they are just numbers. Same as decimal numbers, or binary numbers, I imagine the number wheel, for decimals it goes from 0 to 9, and then for hexadecimals goes from 0 to f.

If you look at the table you will see why hexadecimal is so natural for us, 255
decimal is 0xFF in hex, and after a while you also get used to patterns, e.g. if
it the byte starts with 8 then the first nibble (thats 4 bits, or half a byte)
is 1000, or if it starts with A then the first 4 bits are 1010 and so on. There
are not many patterns between binary and decimal, for example 141 starts with
1000, but 144 starts with 1001. So when you read a sequence 144 157 148, its
hard for you to imagine the bit pattern in your head, while 0x90 0x9D 0x94,
you can "see".
| Decimal | Binary | Hex | Decimal | Binary | Hex | |
|---|---|---|---|---|---|---|
| 0 | 00000000 | 00 | 128 | 10000000 | 80 | |
| 1 | 00000001 | 01 | 129 | 10000001 | 81 | |
| 2 | 00000010 | 02 | 130 | 10000010 | 82 | |
| 3 | 00000011 | 03 | 131 | 10000011 | 83 | |
| 4 | 00000100 | 04 | 132 | 10000100 | 84 | |
| 5 | 00000101 | 05 | 133 | 10000101 | 85 | |
| 6 | 00000110 | 06 | 134 | 10000110 | 86 | |
| 7 | 00000111 | 07 | 135 | 10000111 | 87 | |
| 8 | 00001000 | 08 | 136 | 10001000 | 88 | |
| 9 | 00001001 | 09 | 137 | 10001001 | 89 | |
| 10 | 00001010 | 0A | 138 | 10001010 | 8A | |
| 11 | 00001011 | 0B | 139 | 10001011 | 8B | |
| 12 | 00001100 | 0C | 140 | 10001100 | 8C | |
| 13 | 00001101 | 0D | 141 | 10001101 | 8D | |
| 14 | 00001110 | 0E | 142 | 10001110 | 8E | |
| 15 | 00001111 | 0F | 143 | 10001111 | 8F | |
| 16 | 00010000 | 10 | 144 | 10010000 | 90 | |
| 17 | 00010001 | 11 | 145 | 10010001 | 91 | |
| 18 | 00010010 | 12 | 146 | 10010010 | 92 | |
| 19 | 00010011 | 13 | 147 | 10010011 | 93 | |
| 20 | 00010100 | 14 | 148 | 10010100 | 94 | |
| 21 | 00010101 | 15 | 149 | 10010101 | 95 | |
| 22 | 00010110 | 16 | 150 | 10010110 | 96 | |
| 23 | 00010111 | 17 | 151 | 10010111 | 97 | |
| 24 | 00011000 | 18 | 152 | 10011000 | 98 | |
| 25 | 00011001 | 19 | 153 | 10011001 | 99 | |
| 26 | 00011010 | 1A | 154 | 10011010 | 9A | |
| 27 | 00011011 | 1B | 155 | 10011011 | 9B | |
| 28 | 00011100 | 1C | 156 | 10011100 | 9C | |
| 29 | 00011101 | 1D | 157 | 10011101 | 9D | |
| 30 | 00011110 | 1E | 158 | 10011110 | 9E | |
| 31 | 00011111 | 1F | 159 | 10011111 | 9F | |
| 32 | 00100000 | 20 | 160 | 10100000 | A0 | |
| 33 | 00100001 | 21 | 161 | 10100001 | A1 | |
| 34 | 00100010 | 22 | 162 | 10100010 | A2 | |
| 35 | 00100011 | 23 | 163 | 10100011 | A3 | |
| 36 | 00100100 | 24 | 164 | 10100100 | A4 | |
| 37 | 00100101 | 25 | 165 | 10100101 | A5 | |
| 38 | 00100110 | 26 | 166 | 10100110 | A6 | |
| 39 | 00100111 | 27 | 167 | 10100111 | A7 | |
| 40 | 00101000 | 28 | 168 | 10101000 | A8 | |
| 41 | 00101001 | 29 | 169 | 10101001 | A9 | |
| 42 | 00101010 | 2A | 170 | 10101010 | AA | |
| 43 | 00101011 | 2B | 171 | 10101011 | AB | |
| 44 | 00101100 | 2C | 172 | 10101100 | AC | |
| 45 | 00101101 | 2D | 173 | 10101101 | AD | |
| 46 | 00101110 | 2E | 174 | 10101110 | AE | |
| 47 | 00101111 | 2F | 175 | 10101111 | AF | |
| 48 | 00110000 | 30 | 176 | 10110000 | B0 | |
| 49 | 00110001 | 31 | 177 | 10110001 | B1 | |
| 50 | 00110010 | 32 | 178 | 10110010 | B2 | |
| 51 | 00110011 | 33 | 179 | 10110011 | B3 | |
| 52 | 00110100 | 34 | 180 | 10110100 | B4 | |
| 53 | 00110101 | 35 | 181 | 10110101 | B5 | |
| 54 | 00110110 | 36 | 182 | 10110110 | B6 | |
| 55 | 00110111 | 37 | 183 | 10110111 | B7 | |
| 56 | 00111000 | 38 | 184 | 10111000 | B8 | |
| 57 | 00111001 | 39 | 185 | 10111001 | B9 | |
| 58 | 00111010 | 3A | 186 | 10111010 | BA | |
| 59 | 00111011 | 3B | 187 | 10111011 | BB | |
| 60 | 00111100 | 3C | 188 | 10111100 | BC | |
| 61 | 00111101 | 3D | 189 | 10111101 | BD | |
| 62 | 00111110 | 3E | 190 | 10111110 | BE | |
| 63 | 00111111 | 3F | 191 | 10111111 | BF | |
| 64 | 01000000 | 40 | 192 | 11000000 | C0 | |
| 65 | 01000001 | 41 | 193 | 11000001 | C1 | |
| 66 | 01000010 | 42 | 194 | 11000010 | C2 | |
| 67 | 01000011 | 43 | 195 | 11000011 | C3 | |
| 68 | 01000100 | 44 | 196 | 11000100 | C4 | |
| 69 | 01000101 | 45 | 197 | 11000101 | C5 | |
| 70 | 01000110 | 46 | 198 | 11000110 | C6 | |
| 71 | 01000111 | 47 | 199 | 11000111 | C7 | |
| 72 | 01001000 | 48 | 200 | 11001000 | C8 | |
| 73 | 01001001 | 49 | 201 | 11001001 | C9 | |
| 74 | 01001010 | 4A | 202 | 11001010 | CA | |
| 75 | 01001011 | 4B | 203 | 11001011 | CB | |
| 76 | 01001100 | 4C | 204 | 11001100 | CC | |
| 77 | 01001101 | 4D | 205 | 11001101 | CD | |
| 78 | 01001110 | 4E | 206 | 11001110 | CE | |
| 79 | 01001111 | 4F | 207 | 11001111 | CF | |
| 80 | 01010000 | 50 | 208 | 11010000 | D0 | |
| 81 | 01010001 | 51 | 209 | 11010001 | D1 | |
| 82 | 01010010 | 52 | 210 | 11010010 | D2 | |
| 83 | 01010011 | 53 | 211 | 11010011 | D3 | |
| 84 | 01010100 | 54 | 212 | 11010100 | D4 | |
| 85 | 01010101 | 55 | 213 | 11010101 | D5 | |
| 86 | 01010110 | 56 | 214 | 11010110 | D6 | |
| 87 | 01010111 | 57 | 215 | 11010111 | D7 | |
| 88 | 01011000 | 58 | 216 | 11011000 | D8 | |
| 89 | 01011001 | 59 | 217 | 11011001 | D9 | |
| 90 | 01011010 | 5A | 218 | 11011010 | DA | |
| 91 | 01011011 | 5B | 219 | 11011011 | DB | |
| 92 | 01011100 | 5C | 220 | 11011100 | DC | |
| 93 | 01011101 | 5D | 221 | 11011101 | DD | |
| 94 | 01011110 | 5E | 222 | 11011110 | DE | |
| 95 | 01011111 | 5F | 223 | 11011111 | DF | |
| 96 | 01100000 | 60 | 224 | 11100000 | E0 | |
| 97 | 01100001 | 61 | 225 | 11100001 | E1 | |
| 98 | 01100010 | 62 | 226 | 11100010 | E2 | |
| 99 | 01100011 | 63 | 227 | 11100011 | E3 | |
| 100 | 01100100 | 64 | 228 | 11100100 | E4 | |
| 101 | 01100101 | 65 | 229 | 11100101 | E5 | |
| 102 | 01100110 | 66 | 230 | 11100110 | E6 | |
| 103 | 01100111 | 67 | 231 | 11100111 | E7 | |
| 104 | 01101000 | 68 | 232 | 11101000 | E8 | |
| 105 | 01101001 | 69 | 233 | 11101001 | E9 | |
| 106 | 01101010 | 6A | 234 | 11101010 | EA | |
| 107 | 01101011 | 6B | 235 | 11101011 | EB | |
| 108 | 01101100 | 6C | 236 | 11101100 | EC | |
| 109 | 01101101 | 6D | 237 | 11101101 | ED | |
| 110 | 01101110 | 6E | 238 | 11101110 | EE | |
| 111 | 01101111 | 6F | 239 | 11101111 | EF | |
| 112 | 01110000 | 70 | 240 | 11110000 | F0 | |
| 113 | 01110001 | 71 | 241 | 11110001 | F1 | |
| 114 | 01110010 | 72 | 242 | 11110010 | F2 | |
| 115 | 01110011 | 73 | 243 | 11110011 | F3 | |
| 116 | 01110100 | 74 | 244 | 11110100 | F4 | |
| 117 | 01110101 | 75 | 245 | 11110101 | F5 | |
| 118 | 01110110 | 76 | 246 | 11110110 | F6 | |
| 119 | 01110111 | 77 | 247 | 11110111 | F7 | |
| 120 | 01111000 | 78 | 248 | 11111000 | F8 | |
| 121 | 01111001 | 79 | 249 | 11111001 | F9 | |
| 122 | 01111010 | 7A | 250 | 11111010 | FA | |
| 123 | 01111011 | 7B | 251 | 11111011 | FB | |
| 124 | 01111100 | 7C | 252 | 11111100 | FC | |
| 125 | 01111101 | 7D | 253 | 11111101 | FD | |
| 126 | 01111110 | 7E | 254 | 11111110 | FE | |
| 127 | 01111111 | 7F | 255 | 11111111 | FF |
Examine our micro program b9f1 adf9 b9f1 abf9 b938 b9a9 b9b9 b9b9, each of
those bytes controls various wires connected to the i/o pins on the EEPROM,
either driving them HIGH or LOW, 1 or 0. We actually have 3 programs in
the EEPROMs, 1 for evaluating SUBLEQ programs, 1 for us manually writing the
RAM, in order to punch in the SUBLEQ program for execution, and 1 for us
manually reading the RAM, to see if we messed up.
If you think about low level code, this is the lowest level of code we can write
for this computer, those micro programs controlling the wires, on the most
primitive level, HIGH here, LOW there, .. etc.
Even if it is primitive, it is still a programming language. We have to
transform our ideas into b9f1 adf9.. and so on in order to communicate with
the machine. Quite bizarre, but languages are bizzare. When I am writing this
code, I actually have the computer running in my head, thinking "I will enable
the clock line on the A register, and will have the RAM output on the BUS, so I
will enable the 74LS245 transciever's output, so that A can latch on to the bus
value, that means I have to put 1 on this bit and 0 on that bit, because
74LS245's output control is inverted..". I have to have "empathy" for the
machine. Knowing that everything is possible, how can I express what I think,
into the way it thinks. Empathy to the machine. Theory of mind for the machine.
This the first program written, it was written by Ada Lovelance (Augusta Ada King, Countess of Lovelace), to show how Charles Babbage's Difference engine is more than just a calculation machine, she invented an abstract machine: Analytical engine, and showed that it can do general purpose computation.

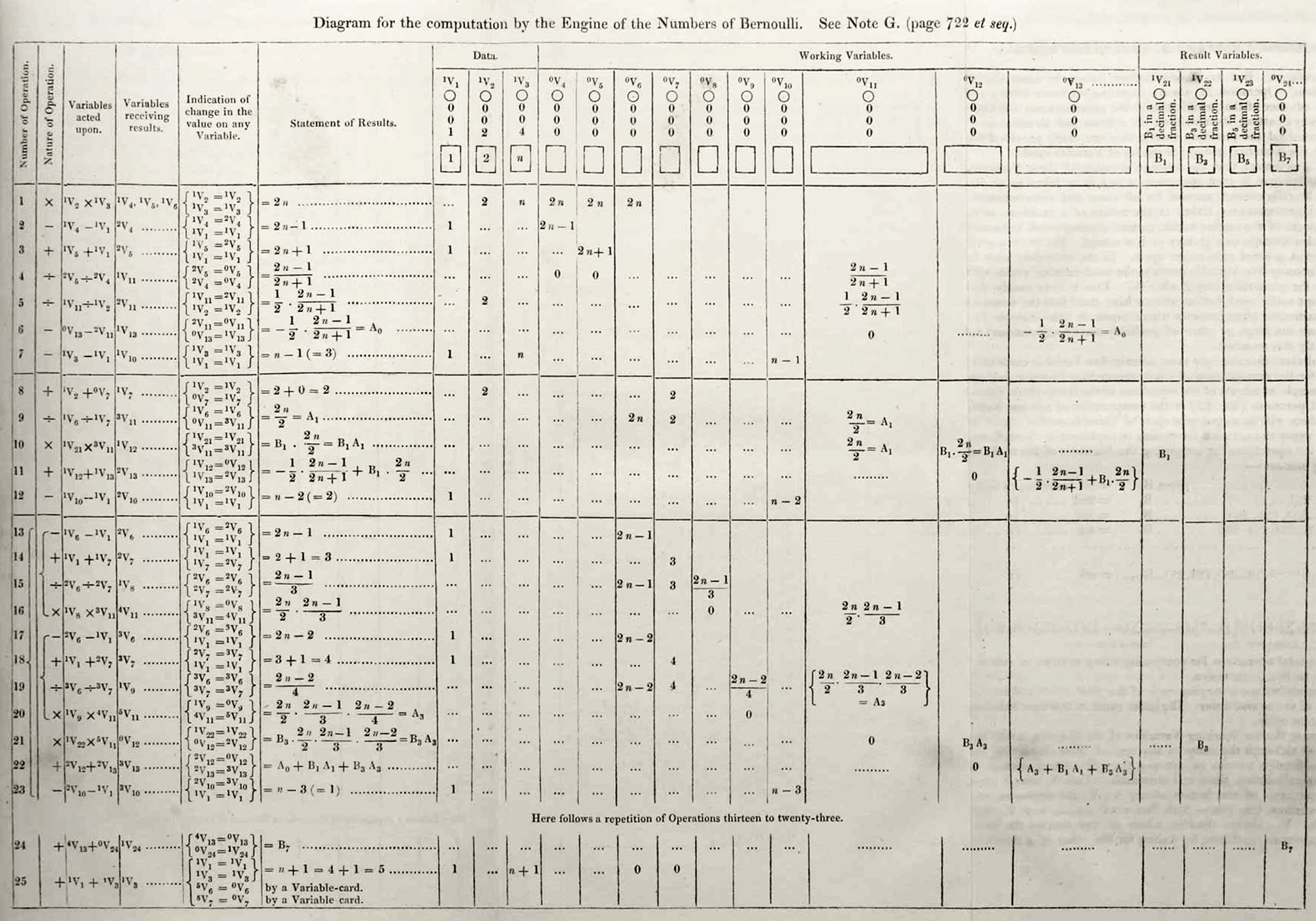
She writes
The Analytical Engine has no pretensions whatever to originate anything. It can do whatever we know how to order it to perform. It can follow analysis; but it has no power of anticipating any analytical relations or truths.
In the end of this book however, I hope to show how it can actually originate everything, but for now lets focus on the It can do whatever we know how to order it to perform part of the quote. You see that the limit is not in what it can do, it is in what you can think of telling it to do. You have to understand it. Like you understand the possibilities of your hand, the limitations of your eyes, the thoughts of your thoughts.
It is very difficult, at least for me, to express my ideas thinking about wire
is HIGH or LOW, so more abstract languages like SUBLEQ make it a tiny bit
easier. Our SUBLEQ program does not know about the wires, it is more abstract,
one level above the control logic, even though it is the machine code for our
computer, it is much easier to write than the micro program of the control
logic.
7 6 9
8 8 0
3 1 0
8 8 9
You can make a computer with completely different design, different parts and wires, and it will should be able to run my SUBLEQ program almost unchanged, I might have to change the addressess if you start from address 200 instead of 0 for example, but at least I wouldn't have to know if you use a temporary register or not for example. Your computer might take 5 clock cycles to execute one instruction, mine takes 10, but this wont matter.
You can see how our SUBLEQ language is one level above the control logic code. We can improve it just a bit by adding labels, like so:
START:
subleq 7,6, END
subleq 8,8, START
subleq 3,3, 0
END:
subleq 8,8, END
This is called an assembly language, it has incredibly close relation to the machine code, but it is easier to write and to read. We can write a program that takes our assembly code and produces actual machine code, replacing the labels with apropriate values.
Now on top of this assembly we can build even higher language that can do more abstract operations:
; Z is a memory location that contains the value 0
; ONE is a memory location that contains the value 1
; .+1 means go to the next instruction address
; Unconditional jump to address c
; Works by subtracting 0 from 0 and jumping to c
JMP c
subleq Z, Z, c ; Z = Z - Z (always results in 0) and jump to c
; Add b to a (a = a + b)
ADD a, b
subleq a, Z, .+1 ; First: Mem[Z] = Mem[Z] - Mem[a]
; Since Mem[Z] is 0, this gives us Mem[Z] = -(Mem[a])
subleq Z, b, .+1 ; Second: Mem[b] = Mem[b] - Mem[Z]
; Since Mem[Z] = -Mem[a], this gives us:
; Mem[b] = Mem[b] - (-Mem[a])
; Mem[b] = Mem[b] + Mem[a]
; So now b contains a + b
subleq Z, Z, .+1 ; Third: Mem[Z] = Mem[Z] - Mem[Z] = 0
; This cleans up by restoring Z to 0
; Move b to a (a = b)
; First clears a, then copies b into it
MOV a, b
subleq a, a, .+1 ; First clear a (a = 0)
subleq b, Z, .+1 ; Z = -b Store negative of b in Z
subleq Z, a, .+1 ; a = a - (-b) Subtracting -b from a (which is 0) gives us b
subleq Z, Z, .+1 ; Clear Z
; Increment a (a = a + 1)
INC a
subleq a, Z, .+1 ; Z = -a Store negative of a in Z
subleq ONE, Z, .+1 ; Z = Z - 1 Add -1 to -a giving -(a+1)
subleq Z, a, .+1 ; a = a - (-a-1) Subtracting -(a+1) from a gives a+1
subleq Z, Z, .+1 ; Clear Z
; Decrement a (a = a - 1)
DEC a
subleq a, Z, .+1 ; Z = -a Store negative of a in Z
subleq ONE, Z, .+1 ; Z = -a - 1 Add -1 to -a giving -(a+1)
subleq Z, a, .+1 ; a = a - (-a-1) Subtracting -(a+1) from a gives a-1
subleq Z, Z, .+1 ; Clear Z
; Branch to c if a is zero (BEQZ a, c)
; Note: Preserves value of a
; Branch to c if b is zero (BEQ b, c)
BEQZ b,c
subleq b, Z, L1 ; If b > 0: Z = -b, continue to next
; If b <= 0: jump to L1
subleq Z, Z, .+6 ; Z = 0, jump after the BEQ
L1:
subleq Z, Z, .+1 ; Clear Z
subleq Z, b, c ; If b = 0: branch to c
; (only reaches here if b <= 0)
Now we can rewrite our program using our higher level language:
START:
DEC 7
BEQZ 7, END
JMP START
END:
JMP END
We keep going up. At each step it is easier and easier for you to think of how to tell the machine what to do.
a = 3
b = 1
start:
if a > 0:
a = a - b
goto start
end:
goto end
Now it is easier for us to think of variables and control flow, you can create much more complicated organizations of code. We keep going up.
a = 3
b = 1
while a > 0:
a = a - b
while:
; just loop forever
Now we have forgotten about the wires. We are just thinking about the code. But
if you zoom in, closely, you will see a = 3 means we have to put 3 somwhere in
memory, and then a = a - b means we have to know where we put the value of a
before, and the value of b, and do SUBLEQ Xb, Xa, Xwhile.
The program is completely separated from the machine, but there are practical implications of understanding the machine. You can see what is slow and fast, what is easy for it and hard for it. Both horses and fish can swim, but they are not equally good at swimming.
Most modern languages are invented, and their inventors are bound by what our computers do well, purely for practical reasons.
The modern computers do not have only 1 instruction like our SUBLEQ computer,
there are many instruction sets, some are very complicated like x86, some are
simpler like RISC-V, you can have instructions that branch if negative, or load
memory into register, store register into memory, multiply, etc.. very fancy
stuff. So the language designers keep that in mind, how to make a language
expressive and productive, so that we can translate our ideas into programs
easilly, with less bugs, and how can we build incredibly complicated
organizations, while thousands of people are working on the same program. And as
you know, no two people are alike.
There are however other kind of languages, that are discovered. And luckily they can also run on our digital computers quite efficiently. Like LISP, lambda calculus, or forth, it seems computation exists in our universe, possibly because is π irrational and our universe is geometric, I don't know, but it seems computation is fundamental force of life, of matter and of our universe.
Do not be limited by our programming languages. They are powerful, and useful, each has its own benefits and pitfalls. But see through them, like Ada Lovelance saw through the wheels and barrels of Charles Babbage's machine, and created the Analytical engine in her mind.
With this the first part of the book is complete. The whole point was for you to
see what is a programming language, to have empathy to the machine and to "see"
the if and the address.
Just for show, here are some examples of the count to 3 program in other languages:
SUBLEQ:
7 6 9
8 8 0
3 1 0
8 8 9
LISP:
(defun countn (n)
(if (> n 0)
(cons n (countn (- n 1)))
nil))
(countn 3)
FORTH:
: COUNTN ( n -- )
BEGIN
1-
DUP 1 <
UNTIL
DROP ;
3 COUNTN
C:
int main(void) {
int a = 3;
int b = 1;
while (a > 0) {
a -= b;
}
}
Brainfuck:
+++[ - ]
All those other languages can be compiled to SUBLEQ, we just have to make the appropriate compiler, which itself is a program that will read the text code (source code), and parse it and convert it to machine code in the best way it knows. Some compilers have very sophisticated techniques and will actually reorder operations or even eliminate code that they know wont be used or does not have effects. The machine code written can be very very different than the code you wrote, and even then, the micro code inside the CPU might also execute the code in a different way, Apple Sillicon chips have more than 600 registers, but expose only 30 or in the machine code available to the compiler. They will actually reorder operations store data in temporary locations in registers instead of memory if it will make the program more efficient and so on. So even the machine code that is written is not the code that is executed.
There are higher order abstractions, like subroutines, functions, objects, messages, classess, reducers, transducers, interfaces and so on. We keep building and piling up on the tower of abstractions. Some are for one to think in, to "empathize" with, others are impossbile. Just like some people see emotions as colors and some have aphantasia and can not imagine pictures when they close their eyes. Do not judge a fish by its ability to climb trees.
Remember, code has to be evaluated and executed. At the moment we execute it on digital computers that have certain properties. All languages, even though they are abstract, in order to be practical, they will leak a bit of the machine into the abstract world. There is immense value in understanding the machine, but you do have to see, like Ada Lovelance, through it.